After Effects Tutorials – Harry Potter Lightning Effects (Priori Incantatem)
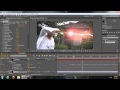
taraartsmovie.blogspot.com Harry Potter Lightning Effects/ Priori Incantatem Tutorial for After Effects SUBSCRIBE for more cool videos and tutorials!
Video Tutorial Rating: 0 / 5
Don’t forget to check out our other video tutorials or share this video with a friend.
0 votes
Loading...19 responses to “After Effects Tutorials – Harry Potter Lightning Effects (Priori Incantatem)”
Leave a Reply
Video Tutorials
Bringing you the best video tutorials for Photoshop, Illustrator, Fireworks, WordPress, CSS and others.
Video tutorial posted 22/12/12
Category: After Effects Tutorials
Pages
Random Videos
-
C# Programming tutorial (1of2)
3,509 views
-
Edit this Portrait In Adobe Lightroom
4,177 views
-
-
Illustrator CS6: Image Trace Improvements
3,889 views
Video Categories
- 3DS Max Tutorials (150)
- After Effects Tutorials (160)
- C# Tutorials (121)
- Colour (6)
- Crazy Effects (1)
- CSS Tutorials (120)
- Dreamweaver Tutorials (139)
- Excel Tutorials (127)
- Featured (10)
- Fireworks Tutorials (131)
- General Effects (9)
- HTML Tutorials (143)
- Illustration and Vector (1)
- Illustrator Tutorials (174)
- IMove Tutorials (119)
- Lightroom Tutorials (145)
- People and Faces (3)
- Photoshop Tutorials (169)
- Text Effects (7)
- Uncategorized (32)
- WordPress Tutorials (140)
Tags
VideoTutorials.co.uk
-
Videotutorials.co.uk offers the web's best Photoshop tutorials, Illustrator video guides, CSS and HTML tutorials and much more all in one place. With new videos being added every day, you can learn how to master software and code to give your images and website some great effects.
Our site has beginner, intermediate and advanced video tutorials of varying lengths so you can learn a new skill at your own speed and level. So whether you're a web designer, print designer or just wanting to edit some family photos, you can get to it quickly and easily using these free video guides. (more)
i know i realized that before, you should check out my video of using some magic stuff
watch again, yes he did.
why doesn’t mine add the key frame help ASAP please is a project for school
Np man 😀
(its awesome 🙂
Thaks so much!
I HAVE THE SOUNDS ON MY CHANNEL
Dumbledore’s Army soundtrack,
your welcome ;)
Yeah i also want to know :(
What’s name song of the video? Please send link.
Btw it is super video!
super effect and tutorial
you serious?
how can i change the flares color?
the name of the program?
Thank you very much.
Sweeeeeeeeeeeeeet.
ok and how do u make the lens flare follow the wand
watch carefully from 6:12
this was good until u didnt show us how to make the lighting follow the wand
i’m downloading adobe after effects right now and i’m filling my time with videos