Macromedia Fireworks mx 2004 Tutorial
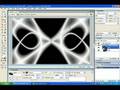
shaun wilsons amazing tutorial on macromedia mx 2004.
Don’t forget to check out our other video tutorials or share this video with a friend.




 0 votes
0 votes19 responses to “Macromedia Fireworks mx 2004 Tutorial”
Leave a Reply Cancel reply
Video Tutorials
Bringing you the best video tutorials for Photoshop, Illustrator, Fireworks, WordPress, CSS and others.
Video tutorial posted 10/12/14
Category: Fireworks Tutorials
Tags: 2004, Fireworks, Macromedia, Tutorial

Pages
Random Videos
Video Categories
- 3DS Max Tutorials (150)
- After Effects Tutorials (160)
- C# Tutorials (121)
- Colour (6)
- Crazy Effects (1)
- CSS Tutorials (120)
- Dreamweaver Tutorials (139)
- Excel Tutorials (127)
- Featured (10)
- Fireworks Tutorials (131)
- General Effects (9)
- HTML Tutorials (143)
- Illustration and Vector (1)
- Illustrator Tutorials (174)
- IMove Tutorials (119)
- Lightroom Tutorials (145)
- People and Faces (3)
- Photoshop Tutorials (169)
- Text Effects (7)
- Uncategorized (32)
- WordPress Tutorials (140)
Tags
VideoTutorials.co.uk
-
Videotutorials.co.uk offers the web's best Photoshop tutorials, Illustrator video guides, CSS and HTML tutorials and much more all in one place. With new videos being added every day, you can learn how to master software and code to give your images and website some great effects.
Our site has beginner, intermediate and advanced video tutorials of varying lengths so you can learn a new skill at your own speed and level. So whether you're a web designer, print designer or just wanting to edit some family photos, you can get to it quickly and easily using these free video guides. (more)




Its Blury :/
when ever i try to draw, fill areas with paint bucket, it dosent let me to
it ( it shows a symbol that is a circle with a diagonlal line through it
Thanks 🙂
I can do all that but i have one problem! The bit at the bottom where it
says play, it doesn’t let me click it! Can anybody help me?
what does macromedia fireworks do?
this was used to make nyan cat
what did u do to make the 2nd copy flip to the other side ?
how do i turn the writing or picture so it goes down the side of a
background
@crazimichael123 0:30 i paste it, then 0:33 i click the black pointer,
click on the image i just pasted and at 0:34, that’s how i flipped it, drag
the line up so it’s diagonally facing the top right hand corner, make it
symmetrical to the other image which is facing diagonally towards the
bottom right corner. Hope that helps
What is it for DVD covers?
great vid, thanks 😀
how do u blend colors?
it orite av got it now cheers
ig to this prorgamme but say i had a normal backroudn colour..lets say
black in stead of it being square corners how do i make then rounded?
please help me someone
i got same problem
how do you blend colors in fireworks? if u answer this question u will get
a sub from me
-.-zZzZZzZz
ur amazing!
wtf